Bulgarian Solitaire

Despite it's name, Bulgarian Solitaire is less an actual game and more a visualization of a mathematical concept in a puzzle or game-like format. Because this visualization is often performed using cards, it is sometimes assumed by people to be another card Solitaire game such as Klondike or FreeCell. However, the game is less a game than a demonstration of a mathematical principle. The rubric described with Bulgarian Solitaire has a number of applications to mathematics and game theory.

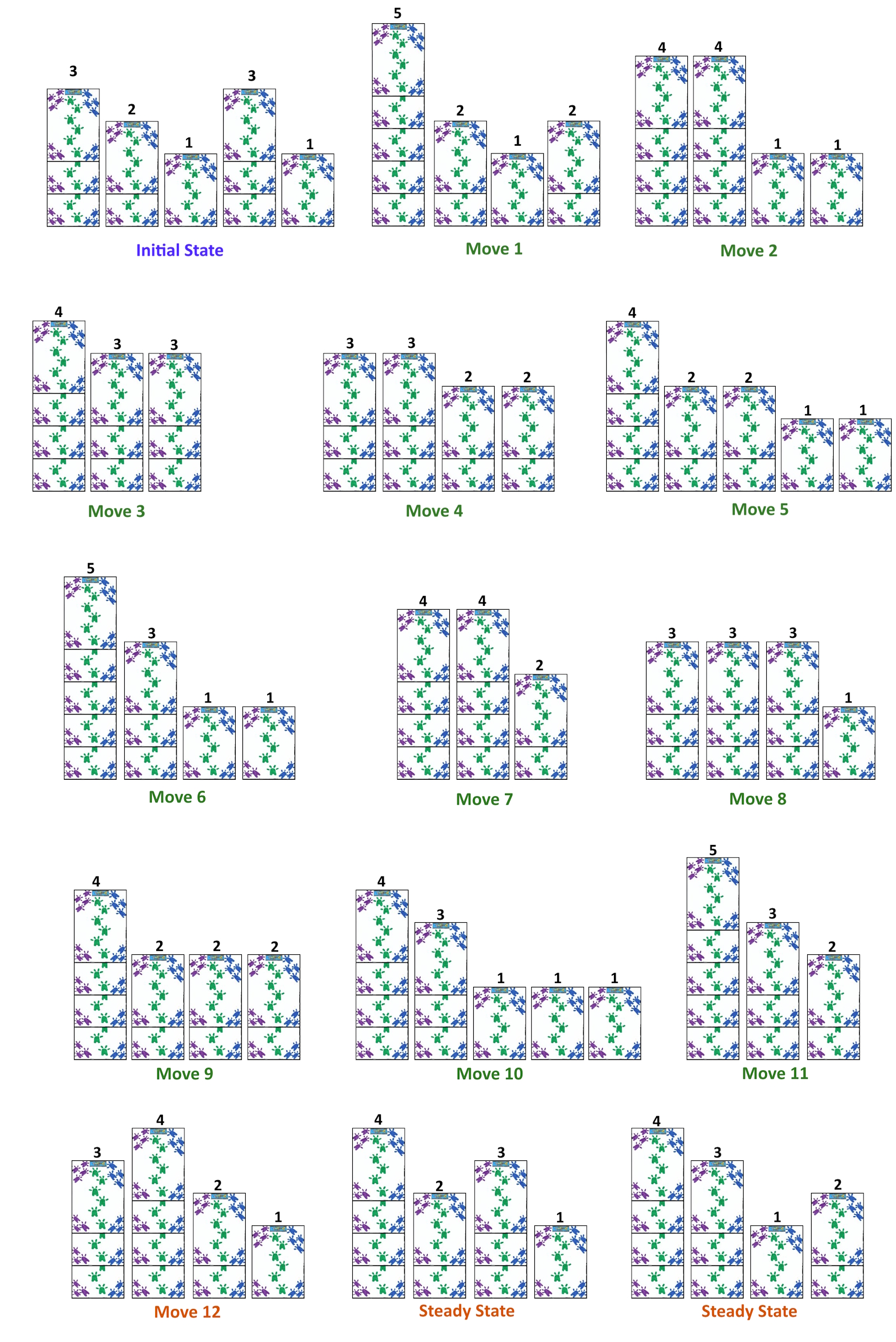Example game of Bulgarian Solitaire in which the player reaches a steady state after 12 moves.

As the legend stands, the original description of Bulgarian Solitaire was published by mathematician David Gardner in 1983, based on a conversation he had in a train while headed to the country of Bulgaria with an unknown stranger. After having the concept described to him, he then proceeded to refine and create the system, calling it Bulgarian Solitaire in honor of the mysterious Bulgarian stranger from whom it was first described.

The puzzle or game starts with a player taking a number of standard cards from a standard deck (or decks) of playing cards. In the original description of the game 45 such cards were used, but really almost any number can be used. Other objects of sufficient quantity can also be used to create these piles, but the game was first described using standard playing cards and is usually easiest to manage and visualize thusly. The suits and ranks of the cards are irrelevant (and the cards are usually used face-down) as the important aspect of the layout thus made is the cards themselves. The cards selected for use are then divided into any number of piles of one or more cards, at the discretion of the player. Thus, the player could have one large pile containing the entire stack selected or a long row of pile, with each pile containing one card each. This then forms the initial layout.

Each move then consists of the player taking the top card from every pile and creating a new pile formed from all the gathered cards. Any piles that consisted of just one card will now be piles of zero cards, and that pile thus eliminated. The new pile created by removing this top card from every pile then forms a new pile which is added to the layout. This action then concludes the move.

This continues until either one of two states are reached in the card layout:

A steady, unchanging state. Each additional move will only result in a state consisting of the same number of piles as the previous state, with these piles containing the same number of cards as that previous state. The relative position of the piles need not be same, but the layout would consist of the same number of piles containing a set number of cards.
A repetitive, terminal cycle. This occurs in the event that the player finds the layout to contain the same layout as from a previous move (but not the state represented by the very last move) as far as the number of piles in the layout and the number of cards in those piles (for example one pile of four cards, a pile of 5 cards and a pile of two cards). The position of the piles relative to each other in the layout does not matter. This state is referred to as a "limit cycle".

Once one of these two states is reached, the game is then over, as any further moves will continue to repeat, with either the unchanging state echoed after each additional move, or a terminal cycle of several moves which is repeated every few moves, in an endless string, with no steady state ever reached.

Although not really a form of solitaire that a player is attempting to win, players will often consider a won game one in which they reach the steady state, and determine how many moves it takes to reach such a state.

This steady state can only be reached in the event that the number of cards (regardless of the number of piles formed) used to start the game is a mathematically triangular number. A triangular number is such a number which can be reached, by starting with 1 and adding each subsequent number in the series until that number is reached. Thus, for a number N, N = 1 + 2 + 3 + .... up to a final number of say, (k), giving the results of N. An example of such a triangular number would thus be ten, which can be reached through 1 + 2 + 3 + 4 = 10. Using such a triangular number (in which N = 1 + 2 + 3 + ... + x), the steady state should be able to reached in x² - x moves or less.

Bulgarian Solitaire is often used in mathematics classrooms to demonstrate triangular numbers and patterns and it's execution is a common programming project in programming courses in schools and Universities. We include Bulgarian Solitaire and it's variants on this site, mainly due to the fact that card players may hear or see the term and be attempting to find it's rules of play.

Since it's initial conception in 1983, a number of other variants of Bulgarian Solitaire have been developed, including the following:

Random Bulgarian Solitaire: Soon after Bulgarian Solitaire's introduction, additional features were added to further explore some of the natural and mathematical facets uncovered. Random Bulgarian Solitaire (also called Stochastic Bulgarian Solitaire), is played similarly to standard Bulgarian Solitaire with one key difference which can greatly influence the number of moves required to reach a final state (although the final state itself will still be directly dependent on the starting number of cards). The difference in Random Bulgarian Solitaire is that instead of removing one card from each pile during a move, there is a random probability (based on a probability P). As an example a player might set p at .50, with thus a 50% probability to remove one card (or not) from that particular pile, repeating for each such pile on each move. Different methods can be used to thus check this probability on each column, such as rolling a die.

Austrian Solitaire: In response to Bulgarian Solitaire, later mathematicians analyzing the Bulgarian Solitaire puzzle developed another a version of Bulgarian Solitaire with an additional variable included (which we will label as L). This variant is called Austrian Solitaire.

Austrian Solitaire starts very similarly to Bulgarian Solitaire with the player taking a deck of any number of cards and arranging this deck into some number of piles (containing one or more cards per pile). The player next then takes one card from each pile. Then using the cards from this pile of drawn cards, he creates new piles containing exactly a number of cards equal to L, creating as many such piles as he can and adding these to the layout. Any leftover cards that cannot so be added to the layout (being less than the number needed to create one additional pile of size L) are set aside in the "hand", and will be added to the pile of gathered cards from the next turn. The player continues making additional moves until reaching either a steady consistent state or forming a repeating cycle of moves (limit cycle).

Due to the inclusion of this additional variable L and the rules governing it, the outcome of the game may not be as obvious or predictable from the starting number of cards and initial layout.